Yield Curve
What is Yield Curve and how is it used for analyzing the economy?
The Yield Curve is a graphical representation of the yields of multiple bonds which have different maturities. This is an important concept in Bond markets as it can provide an idea about the market perception of the risks associated with the bonds of different maturities.
This graph is usually built for the Government Securities and it is also called as the Treasury Yield Curve. Since the Government Bonds are traditionally considered to be risk-free assets, the Yield Curve also acts as a benchmark for other lending rates in the economy.
When creating a Yield Chart, the y-axis in the graph will represent the Yield to Maturity of the Bond and the x-axis will represent the time to maturity of the bond. To obtain a Yield Curve, the yields of multiple bonds with different maturity dates have to be plotted on the graph.
Yield to Maturity (YTM)
The most effective method for measuring the bond yields is to use the concept of Yield to Maturity (YTM). Depending on the maturity of the bond, the investors will receive Coupon payments at regular time intervals across the years.
Due to the concept of Time Value of Money, the Coupon payments received today are considered to be more valuable than the Coupon payments received in the future. So, the Yield to Maturity can give an accurate measurement of the actual investment returns that will be generated by a Bond.
When measuring the YTM of any bond, the first step is to predict the Cash Flow from the bond (the coupon payment schedule). The YTM will be the Discount Rate which is used to get the Present Value of all the future Cash Flows. The sum of all these Discounted Cash Flows will be equal to the current price of the bond.
Sample calculation
Let us assume that the current trading price of the bond is INR 850. We want to find the YTM, if an investor buys the bond at this price. The borrowing terms of the Bond are as follows:
Tenure: 3 years
Face Value: INR 1,000
Interest: 9 %, paid annually
The Cash Flows for this bond will be as follows: INR 90 after year 1 (9% of INR 1,000), INR 90 after year 2 and INR 1,090 after year 3. Assuming annual compounding, the equation that we need to solve for finding the YTM is given below.
\(850=\frac{90}{(1+YTM) }+\frac{90}{(1+YTM)^2} +\frac{1,090}{(1+YTM)^3}\)The value can be calculated by using the ‘RATE’ function or ‘Solver’ feature in MS Excel (Refer: How to use Solver in Excel?). By solving the above equation, we get a YTM of ~ 0.1564, which means ~ 15.64 % yield.
Building the Yield Curve Chart
The yield of the bonds will change when the Last Trade Price of the bonds will move. For example, if the price of a bond drops, then the yield will go up. And if the price of the bond increases, then the yield will go down.
At any given time, multiple bonds with different maturities trade simultaneously in the markets. Depending on the economic scenario, the yields can be different for each maturity. So, the shape of the Bond Yield Curve will be governed by the supply and demand in the market. (Refer: How market prices affect yield of bonds?)
Example: Suppose that the Economy in a developing country is very poor and the investors expect that the government might default in the future. In such a case, the long-term bonds with maturity of 10 years might be riskier than the bonds with a maturity of 3 months. So, the yield of the 10-year bond will be much higher than the yield of the 3-month bond.
Plotting the Yield Curve Graph
Once the yields of all the bonds have been calculated, the next step is to plot these values on the chart. The yield is represented on the y-axis and the time to maturity is indicated on the x-axis. The chart will give a better idea when the number of data points is large.
The Yield to Maturity or the Current Yield could be used to build the curve. As already mentioned before, the yields of the bonds will keep changing based on the trading that happens in the bonds. So, the shape of the curve will not be constant and the whole chart has to be updated regularly, as per the latest data.
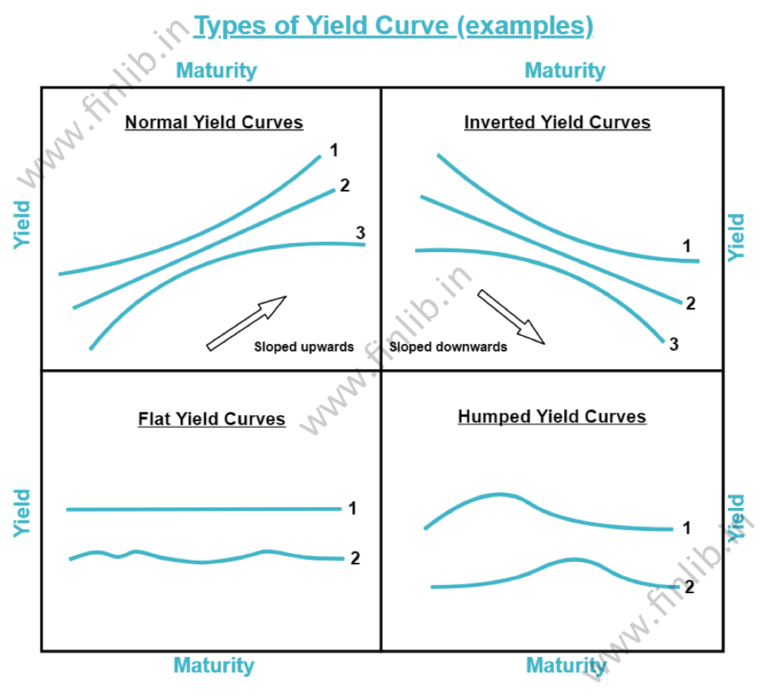
Types of Yield Curve
The shape of the curve will depend on the short-term and long-term Bond Yields. Some of the most popular shapes of the curve can be seen in the below Bond Yield Charts. The below shapes have been used as examples to explain the idea. The actual shapes in the real world might not be so smooth.
1. Normal Yield Curve
In case of a Normal Yield Curve (also called Positive Yield Curve), the bond yields in the long-term will be higher than the bond yields in the short-term. So, the curve will be sloped upwards and it usually indicates that the economy is expected to grow.
This curve is considered as normal because there is a higher risk and uncertainty associated with the bonds that will be expiring after a long time. And there would be a lower risk of default on the bonds that are expiring within the next few months. So, it is natural that the yields of long-dated securities will be higher.
2. Inverted Yield Curve
If a Yield Curve is inverted, then it means that the long-term yields are lower than the short-term bond yields. The shape of the curve will be sloped downwards in this case. A Yield Curve Inversion means that there is stress in the short-term. It is also called as a Negative Yield Curve.
Due to uncertainty in the near-term, the investors tend to buy safe assets like long maturity bonds. This causes the price of the long-term bonds to increase and their yields to drop. So, an inverted curve usually indicates a recession (or possibility of a recession) in the near future.
3. Flat Yield Curve
The Curve will be considered to be flat when all the bonds with different maturities will have a similar yield. So, the slope of this type of curve is usually close to Zero because the values of the yield will be very close to each other.
This type of curve means that the yields have a near-zero sensitivity towards the time duration. It often indicates that the economic growth is under stress and there is high uncertainty about the future.
4. Humped Yield Curve
This type of curve is a bit similar to a Flat Curve mentioned above because the short-term and long-term yields are approximately same. However, in this case, the medium-term bond yields are usually a bit higher and that gives a small hump shape in the graph.
5. Steep Yield Curve
When we are talking about the steepness, the focus is on the slope of the curve and not on the direction of the curve. So, this term could be used for both Normal and Inverted curves.
A curve having a large steepness will usually mean that there is a big difference in the short-term and long-term bond yields. Whereas a smaller slope will indicate that the difference between the bond yields is lower.
Yield Curve Risk
The Yield Curve of a country / region is actively used as a reference for pricing the bonds in that region. So, any change in the shape of the curve will impact the bond prices. This shift or change in the curve is known as the Yield Curve Risk and it can impact all Fixed Income securities.
There could be multiple reasons for a Yield Curve to change in shape or shift in position. Some of the common causes are:
Actions by Central Banks (Interest rate changes, Open Market Operations etc.)
Change in economic growth forecasts
Possibility of recession
Increase / decrease in borrowing by the government
Wars, disasters and other high-impact events
etc.
If there is a parallel shift in the Yield Curve by 20 Basis Points, then we can say that the yield for all the bonds has shifted by 20 Basis Points. But in real life, the shift might not be uniform for all the time periods.
Example: Bonds with 6-month maturity might shift by 10 Basis Points and the bonds with 5-year maturities might have shifted by 25 Basis Points. In this example, the shape of the curve will change.
Disclaimer
- This page is for education purpose only
- Some information could be outdated / inaccurate
- Investors should always consult with certified advisors and experts before taking final decision
- Some images and screenshots on this page might not be owned by FinLib