How to use Solver in Excel?

What is Solver in Excel and how is it used for optimization and calculations?

Microsoft Excel is a great tool which can be used for data compilation and analysis. There are many formulas pre-defined in the software for easily performing operations on the data. In addition, it also provides other tools for mathematical calculations.

The Solver in excel is a great feature which helps in iteratively solving the equations and performing basic optimization studies. So, it can be used to find the maximum or minimum value of a variable, depending on the formulas applied in the cells.

When using Solver in Excel, there are primarily 3 types of variables/cells that have to be defined:

1. Decision Variables/cells (These are the cells for which the values will be changed)
2. Constraint Variables/cells (These are optional conditions that can be defined when changing the values in the Decision cells)
3. Objective cell (This is the target value that the Solver will try to achieve, by changing the Decision cells)

Excel Solver example

Suppose that we want to maximize the below equation,

\(20x +13y\)

Such that,
\( x + y <= 10 \)
and \( x, y >= 0 \)

Here,
\(20x+13y\) is the Objective, and Solver will try to maximize this value
\(x\) and \(y\) are the Decision Variables, which will be changed to maximize the above value
\(x + y <= 10\) and \(x, y >= 0\) are the restrictions that the Solver tool will consider when selecting the values for \(x\) and \(y\)

How to add Solver in excel?

Before you can use the Solver feature in excel, it is important to activate the Solver add-in plugin. To check if this add-in is already activated in your version of excel, simply go to the ‘Data’ tab and look for the ‘Solver’ button in the ‘Analyze’ section. (In Excel 97 and Excel 2003, the Solver button would show up in the ‘Tools’ menu)

Steps to add the Excel Solver button

If the button is not present, then it has to be activated first. Just follow the below-mentioned steps for Excel 2007 and later versions. (For Excel 97 and 2003, the button can be activated by clicking on ‘Add-Ins’ option in the ‘Tools’ menu)

Step 1A: Click on the ‘File’ menu on the top-left corner and then select ‘Options’.

For Excel 2007, click on the Microsoft Office button on the top-left corner and click on ‘Excel Options’.

Then,

Step 2A: In the new window that opens, click on the ‘Add-ins’ menu.

Then, select the option ‘Excel Add-ins’ from the Manage drop-down menu and click on the ‘Go…’ button.

Step 3A: From the list of Add-ins that are displayed in the new window, select the ‘Solver Add-in’ option and click on the OK button. In some cases, a message will be shown that that the add-in has to be first installed on the machine. Click on the ‘Yes’ button in the warning message to install the add-in.

If the ‘Solver Add-in’ is not displayed in the list of available add-ins, then click on the ‘Browse’ button to manually locate the add-in from your computer.

Once the Excel Solver add in has been included, you might be required to restart the Excel software or the machine. After that, the ‘Solver’ tool will display in the ‘Data’ menu/tab. In Excel 97 and Excel 2003, it would show up in the ‘Tools’ menu.

Solving methods in Excel Solver

When using the Solver in Excel, there are 3 different solving methods. The technique to be used will depend on the problem and the type of equations that are being handled.

1. Simplex LP

This method refers to the Linear Programming method of finding the Global Optimal Solution. This technique can be used when the objective and constraints are linear equations, which contain the Decision Variables.
The Example 1 mentioned in the next section has linear equations. So, it is possible to use the ‘Simplex LP’ solving method in that case.

2. GRG Nonlinear

The GRG Nonlinear method in Solver refers to the Generalized Reduced Gradient algorithm, which is used to find the optimal solution. This technique works well when the objective and constraints are non-linear and smooth functions.
If all the equations are Convex in nature, then this method will give the Global Optimal Solution. But if the equations are not convex, then this method will only give a Local Optimal Solution.
The Example 2 in the next section has non-linear equations and we would need to use the GRG Nonlinear method of solving.

3. Evolutionary

This method is used when the objective and constraints are non-smooth and non-convex functions. When using this option, only an approximate value can be achieved as it is not possible to find the local or global Optimal Solution.

A common scenario when this method can be used is where the data contains multiple If-Else conditions.

How to use Solver in Excel?

The first step when using Solver in Excel is to structure the data properly and create accurate labels and references. The values in the Constraints and the Objective cells should be calculated by using formulas and it should not contain static values.

Let us look at some Excel Solver examples by using some common scenarios in Finance.

Example 1: Basic Optimization problems in companies

Suppose that a company has 2 products and it generates a profit of INR 100 by selling product A and a profit of INR 75 by selling product B. The company has 120 employees and it takes 3 workers to manufacture product A and 2 workers to manufacture product B.
Let us assume that the company can build a maximum quantity of 50 Finished Products (A or B) in 1 month. We want to maximize the profit by finding out the right mix of the number of items that should be built of A and B each.

Solution: Let us assume that ‘A’ is the quantity manufactured of product A and ‘B’ is the quantity manufactured of product B. To maximize the profit, we need to find the optimum value of A and B by solving the below-mentioned equations:

Maximize: 100A+75B

Such that,
3A + 2B <= 120 (Restriction on the total number of workers)
A + B <= 50 (Restriction on the total number of items in a month)
A, B >= 0 and A, B are integers

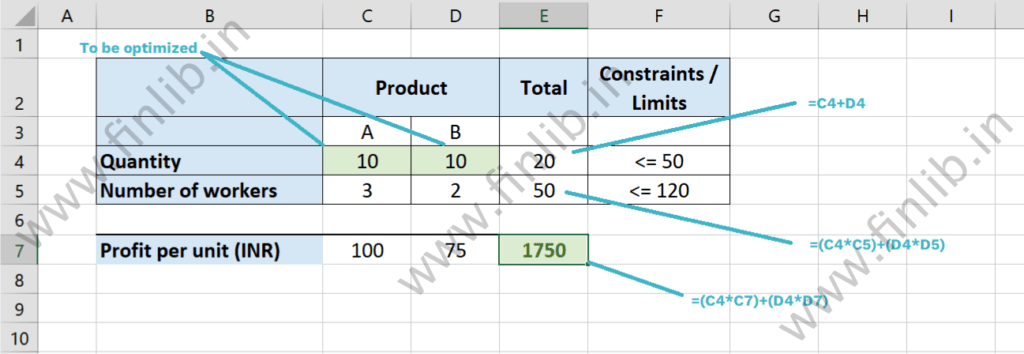
Step 1B: When we put these equations in the different cells in Microsoft Excel, the file might look something like this:

As it can be seen in the above image, formulas have been used in the Constraint Cells (E4 and E5) and in the Objective Cell (E7). The Decision Variables are in cells C4 and D4. The values in column F are the constraints, which are only for reference purposes here.

In simple terms, the Solver will try to maximize the value of cell E7 by changing the values in cells C4 and D4. At the same time, the Solver will make sure that the values in E4 and E5 are within the defined constraints.

Step 2B: Click on the ‘Solver’ button in the ‘Data’ tab.

In the new window that opens, enter the objective cell in the text box and select the ‘Max’ or ‘Min’ option to maximize or minimize the Objective Cell. A fixed value could also be entered in the ‘Value Of:’ text box. (We are trying to Maximize the value of cell E7)

Next, enter the cells that have to be changed in the ‘By Changing Variable Cells:’ text box. Instead of typing, this can also be done by clicking on the text box and then selecting the cells in Excel by using the mouse. (We are trying to find optimum values for cells: C4 and D4)

Next, add the constraints in the ‘Subject to the Constraints:’ section by using the ‘Add’ button. When ‘Add’ is clicked, a new window will open where the constraints can be entered. In the drop-down menu, the ‘int’, ‘bin’ and ‘dif’ options refer to the ‘Integer’, ‘Binary’ and ‘All Different’ types of data, respectively.

(In the below image, we are defining the restriction on the total quantity of products: A + B <= 50)

Similarly, all the constraints can be managed by using the ‘Add’, ‘Change’ and ‘Delete’ buttons. If applicable, tick the option: ‘Make Unconstrained Variables Non-Negative’. Since the number of products manufactured cannot be negative, we have selected this option in the below image.

Choose one of the options from the ‘Select a Solving method:’ drop down menu. Since the equations in this example are Linear, they can be solved using Linear Programming. So, we have used the ‘Simplex LP’ option.

The final data in the Solver window will look something like this:

Click on the ‘Solve’ button when all the data has been entered.

Step 3B: If the Solver in Excel is able to find an optimal solution, then the values in the variable cells will be changed and a new window will open up. In this window, the user can select one of these 2 options:

‘Keep Solver solution’, to accept the changed values
Or
‘Restore Original Values’, to revert the changed values and go back to the Solver window. The user can then make changes to the parameters by repeating Step 2B, mentioned above.

Click on the ‘OK’ button after selecting one of the above 2 options.

However, if there was an error when solving the equations, then a message will be shown that ‘Solver could not find a solution’.

Step 4B: If the Solver solution has been accepted, then the user will notice that the values in the Variable Cells will be changed. In our example, the Solver has recommended to manufacture 20 units of Product A and 30 units of Product B. And as calculated, the maximum profit that can be achieved is INR 4,250 (cell E7).

Example 2: Calculate Yield to Maturity using Solver feature

Suppose that we are trying to find the 10-Year Bond Yield for a Government Security which has the below-mentioned borrowing terms:
Face Value: INR 100
Interest payment: 6 %, paid semi-annually
Tenure: 10 years

Let us assume that in the auction, the bond is purchased for INR 90. We can find the Yield to Maturity (YTM) by using the Solver in Excel.

Solution: The Cash Flows for the above bond will be as follows:
INR 3 at end of 6 months ((6% of INR 100) / 2),
INR 3 at end of year 1,
INR 3 at end of 1.5 years,
…and so on…
INR 3 at end of 9.5 years,
INR 103 at the end of year 10.

These Cash Flows can be discounted to get the present value of the bond. So, we are basically trying to find the value of \(YTM\) in the below-mentioned equation.

\(90=\frac{3}{(1+YTM)^{0.5}} +\frac{3}{(1+YTM)^{1}} +\frac{3}{(1+YTM)^{1.5}} + ……. +\frac{103}{(1+YTM)^{10}}\)

Manually solving the above equation is very difficult. So, the Excel Solver can be used to calculate a fairly accurate value of the yield. The same technique can be used to find the Internal Rate of Return (IRR) of an investment, by discounting the Cash Flows.

Step 1C: When we put the values in different cells in Microsoft Excel, the file structure might look something like this:

In column C, we can see the Cash Flows at the different time instants (defined in terms of years, in column B). In column D, the Cash Flows are discounted to the present date. A dummy Discount Rate of 10 % (defined in cell F9) has been used to get the Discount Factor.

By taking a sum of all these Discounted Cash Flows, we can get the Present Value of the Bond. The Solver will try to make the value of cell D23 equal to INR 90, by changing the value of cell F9. (INR 90 is the price at which the Bond was purchased)

Step 2C: Click on the ‘Solver’ button in the ‘Data’ tab.

In the new window that opens, enter the objective cell in the ‘Set Objective:’ text box and select the target value of the Objective Cell in the ‘Value Of:’ text box. (We are trying to make the value of cell D23 equal to INR 90)

Next, enter the cells that have to be changed in the ‘By Changing Variable Cells:’ text box. Instead of typing, this can also be done by clicking on the text box and then selecting the cells in the Excel by using the mouse. (We are trying to find the value for cell F9)

Choose one of the options from the ‘Select a Solving method:’ drop down menu. Since the equations in this example are not Linear, they cannot be solved using the ‘Simplex LP’ option. So, we have to use the ‘GRG Nonlinear’ option instead.

The final data in the Solver window will look something like this:

When all the data has been entered, click on the ‘Solve’ button.

Step 3C: If the Solver in Excel is able to find a solution, then the values in the Variable Cells will be changed and a new window will open up. In this window, the user can select one of these 2 options:

‘Keep Solver solution’, to accept the changed values.
Or
‘Restore Original Values’, to revert the changed values and go back to the Solver window. The user can make changes to the parameters by repeating Step 2C, mentioned above.

Click on the ‘OK’ button after selecting one of the 2 options.

Step 4C: If the Solver solution has been accepted, then the user will notice that the values in the Variable Cell will be changed. In our example, the Solver has calculated the value of Yield to Maturity (YTM) as ~ 7.57% (cell F9).

However, if there was an error faced by the Solver in Excel, then a message will be shown that ‘Solver could not find a solution’. For example, if we try to use the ‘Simplex LP’ method to solve the equation in this example, then the following error message will be displayed: ‘The linearity conditions required by this LP Solver are not satisfied’.

In this case, since the equation is non-linear, the only option is to use the ‘GRG Nonlinear’ or ‘Evolutionary’ method. Select the option ‘Return to Solver Parameters Dialog’ and click on the ‘OK’ button to return to the Solver menu (and repeat Step 2C, mentioned above).

In this example, since the functions are smooth and non-linear, we can use the GRG Nonlinear method in Solver Excel for solving the equation.

Disclaimer

• This page is for education purpose only
• Some information could be outdated / inaccurate
• Investors should always consult with certified advisors and experts before taking final decision
• Some images and screenshots on this page might not be owned by FinLib